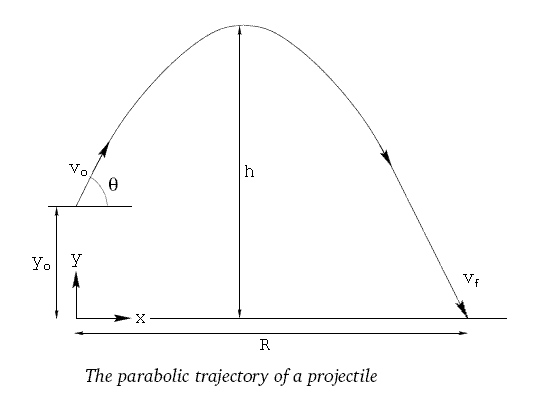
The motion of an object moving near the surface of the earth can be described using the equations:

(1): x = xo + vxo·t

(2): y = yo + vyo·t - 0.5·g·t2

The calculator solves these two simultaneous equations to obtain a description of the ballistic trajectory. The horizontal and vertical components of initial velocity are determined from:

vxo = vo·cos θ

vyo = vo·sin θ

Then the calculator computes the time to reach the maximum height by finding the time at which vertical velocity becomes zero:

vy = vyo - g·t

trise = vyo/g

Maximum height is obtained by substitution of this time into equation (2).

h = yo + vyo·t - 0.5·g·t2

Next, the time to fall from the maximum height is computed by solving equation (2) for an object dropped from the maximum height with zero initial velocity.

0 = h - 0.5·g·t2

tfall = √(2·h/g)

The total flight time of the projectile is then:

tflight = trise + tfall 

From this, equation (1) gives the maximum range:

range = vxo·tflight

The projectile speed at impact v_f is determined by applying the Pythagorean Theorem:

vf = √(vxf2 + vyf2)

In which:

vxf =  vxo

vyf = -g·tfall

Copyright © 2004, Stephen R. Schmitt